Optimización y modelado multifísica
Áreas
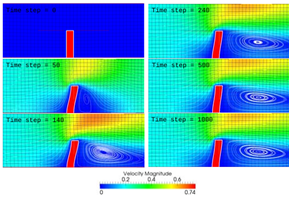
Cuando se trabaja con la resolución de ecuaciones diferenciales parciales en dominios en movimiento, como son los problemas en el área de la interacción fluido-estructura (FSI Fluid Structure Interaction), una de las formulaciones más utilizadas es la denominada Lagrangiana-Euleriana Arbitraria (ALE Arbitrary Lagrangian-Eulerian). Cuando se utiliza una formulación ALE, las ecuaciones de gobierno deben reescribirse y se introducen términos adicionales relacionados con la velocidad y la posición de la malla o dominio discretizadado. Las ecuaciones reformuladas deben integrarse en el tiempo. La forma común de proceder es utilizar un esquema clásico de avance en el tiempo como la familia theta o la familia de fórmulas diferenciales hacia atrás (BDF Backward Differentiation Formula). En este contexto surge la Ley de Conservación Geométrica Discreta (DGCL Discrete Geometric Conservation Law). En este plan proponemos desarrollar una nueva metodología para desarrollar formulaciones que cumplan la DGCL para sistemas advectivo-difusivos generales en dominios en movimiento utilizando un esquema ALE. Esta metodología se aplicará a la familia theta de métodos de integración temporal y también como una extensión a la BDF de tres puntos. También se desarrollarán esquemas de acoplamiento entre códigos fluido-dinámicos (Ej. Code_Saturne) y códigos estructurales (Ej. Code_Aster) para la resolución de problemas de interacción fluido estructura, tanto desde el punto académico y como de las aplicaciones industriales.
Personal involucrado en la línea de investigación: Mario Storti (Investigador Principal); Luciano Garelli (Investigador Adjunto); Gustavo Ríos Rodríguez (Investigador Adjunto);
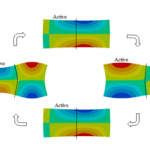
El CIMEC desarrolla simulaciones de componentes mecánicos compuestos por materiales piezoeléctricos por medio del método de los elementos finitos, manteniendo estrecha relación con el Instituto de Investigaciones en Ciencia y Tecnología de Materiales (INTEMA) División Cerámicos, ubicado en la ciudad de Mar del Plata, para la validación con resultados experimentales de los modelos numéricos que se propongan.
Personal involucrado en la línea de investigación: Alberto Cardona (Investigador Superior); Federico Cavalieri (Investigador Adjunto); Leandro Ramajo (INTEMA)